Простая эпидемическая модель
Рассмотрим простую эпидемическую модель, в которой предполагается, что произвольный узел сети, состоящей из постоянного количества (N) компьютеров, может находиться только в двух состояниях: уязвимом (S) и инфицированном (I). S + I = N. Предположим, что на каждом инфицированном узле может существовать только одна копия червя, которая случайным образом выбирает в доступном адресном пространстве потенциальную жертву с опять-таки средней постоянной скоростью b в единицу времени (на поиск и заражение одной жертвы в среднем тратится 1/b секунд). В простейшем случае b определяется средней скоростью сканирования червем сети (Vs) и размером её адресного пространства (Nip):

(Согласно спецификации IP4 Nip = 232.)
Введя переменные i = I/N и s = S/N, получим уравнение динамики доли инфицированных узлов:

Уравнение (2) имеет аналитическое решение. Предполагая, что в начальный момент времени t0 = 0 доля инфицированных узлов составляет i0, получим зависимость:

из коей вытекает, что эпидемия в принятой модели полностью определяется двумя параметрами: скоростью размножения червя (b) и начальной зараженностью рассматриваемой сети (i0).
(3) – это логистическая функция, которая только по форме отличается от результата [17], где постоянная интегрирования определена через константу по времени, а не через начальную зараженность, как в нашем случае. Из приведенных в [17] данных следует, что для Code Red v2 i0 ~10–11…10–10, т.е. можно предполагать, что червь начинал атаку на Сеть с одного компьютера.
Динамика функции (3) характеризуется тремя четко различимыми этапами (Рис. 1).
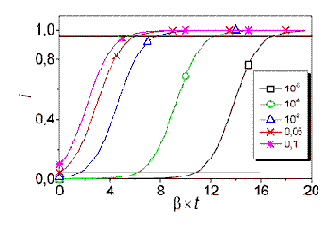
Рис. 1. Развитие эпидемии в зависимости от начальной зараженности сети. Время представлено в единицах b ? t (т.е. периодах размножения).
1-й этап – сравнительно медленное (но тем не менее экспоненциальное) нарастание зараженности до порогового уровня iпор » 0,05 (красная горизонтальная прямая на Рис. 1). Скорость удвоения доли пораженных машин равна ln(2)/b.
2-й этап – взрывная фаза (outbreak) в диапазоне 0,05 < i < 0,95. Продолжительность её определяется только скоростью поиска b и приблизительно равна 5,89/b.
3-й этап – насыщение, i > 0,95 (черная горизонтальная прямая на Рис. 1). На этом участке при случайном сканировании адресного пространства зараженные узлы контактируют преимущественно друг с другом, поэтому уцелевшие узлы могут оставаться «чистыми» неопределенно продолжительное время.
Для достижения порога насыщения i=0,95 требуется время

из чего следует, что динамика эпидемии не зависит от масштабов сети (в пределах применимости рассматриваемой модели). К примеру, сеть из миллиона компьютеров, в которой в начальный момент времени будет инфицирован один узел, будет практически полностью заражена за то же время, что и аналогичная сеть из ста миллионов компьютеров, где в начальный момент окажется 100 «червивых» узлов.
Из полученных результатов вытекает, что:
1. Однородность Сети относительно определенной уязвимости представляет главную угрозу [22]. Практика показала, что даже черви, которые выбирают жертву случайным образом и, следовательно, являются самыми медленными [17], за считанные минуты способны поразить ключевые узлы Интернета и вывести из строя телекоммуникации на уровне отдельных стран [23]. Таким образом, любая структура деятельность которой критически зависит от доступа к Интернет (либо, наоборот, нормальное функционирование Интернет зависит от работоспособности таковой структуры), должна иметь резервные системы, построенные на программном обеспечении с различающимся кодом.
2. Экспоненциальный рост количества вирусов в любой сети свидетельствует об отсутствии защитных механизмов либо о полной их неэффективности.
3. Механизм случайного выбора жертвы ограничивает снизу скорость распространения вирусов по сети. Значительно повысить её можно достаточно простыми средствами: подготовкой предварительного списка адресов для атаки, сканированием подсетей, выделением каждой копии червя отдельного фрагмента сетевого адресного пространства, поиском подходящих мишеней на зараженном компьютере и др. [17]. Если, к примеру, копия червя получает в наследство только непересекающуюся половину адресного пространства от «родителя», то из (1) следует, что это эквивалентно удвоению скорости заражения каждые 1/b секунд (Рис. 2).
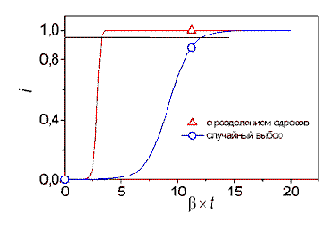
Рис. 2. Ускорение эпидемии при выделении каждой копии червя своего непересекающегося фрагмента адресного пространства.
4. Инфекционная способность b в значительной степени зависит от скорости прохождения сетевых пакетов. Современные Web-приложения ориентированы на передачу огромных массивов данных (к примеру, видео), поэтому широкополосный доступ к Интернет становится насущной необходимостью, что автоматически повышает скорость распространения червей.
5. Системы раннего оповещения о развитии эпидемии окажутся сколько-нибудь эффективными только на участке i << iпор и при крайне низких значениях b. Моделирование распространения Code Red и Slammer показало, что анализ обращений к несуществующим адресам позволяет определить признаки вирусной активности в сети при заражении 1–2 % уязвимых узлов [24]. Таким образом, предупреждение может быть получено максимум за 1,65/b секунд до достижения порога взрыва iпор. Согласно данным [24] в случае Code Red это время составило бы не более 50 минут, а для Slammer не превысило бы 15–20 секунд. Очевидно, что в обоих случаях эпидемии можно было бы только зафиксировать, но не предотвратить.
5. Эффективность сетевых эпидемий можно значительно повысить, проводя скрытное предварительное заражение отдельных уязвимых узлов.Чем ближе i0 к iпор, тем разрушительнее могут оказаться последствия вирусной атаки (Рис. 1 ).
6. Увеличение адресного пространства Nip понижает инфекционную способность червей со случайным выбором жертвы. IPv6 предполагает 2128 адресов и это может несколько уменьшить темпы нарастания эпидемий, если адреса окажутся достаточно равномерно «размазаны» по всему пространству.
Анализ эпидемий Code Red v2 и Slammer на основе простой модели показал удовлетворительно совпадение с реально наблюдаемой динамикой эпидемий. Уже Code Red v2, чья инфицирующая способность оценивалась по различным данным от 0,7 до 1,8 компьютера в час менее чем за половину суток мог получить контроль над сотнями тысяч серверов. В то же время Slammer при скорости удвоения 8,5 секунд имел инфицирующую способность ~293 узлов в час и мог проникнуть на 90% уязвимых компьютеров всего лишь за 10 минут.